To correctly interpret sensory data, the brain is faced with solving an inverse problem: one where the causes need to be inferred from the perceived outcomes [1]. There are many different computational models and explanations for how the brain codes information and understands its environment. Bayesian predictive coding, the combination of Bayesian inference and predictive coding, is one such model [2, 3, 4, 5]. Although probabilistic representations are not new, Bayesian predictive coding has become increasingly popular in the field of cognitive neuroscience over the last few decades [2]. This model has made important contributions to our understanding of nearly all areas of cognition, including perception, reasoning, and learning [2]. Bayesian predictive coding is not used in conflict with other methods in computational neuroscience but rather as a novel, complementary perspective that is often very useful [3]. Inference on its own only provides a method for computing predictions and does not specify the neural representations those predictions have [4]. This is why Bayesian inference and predictive coding go well together. Predictive coding uses the inferences to create prediction errors, which the brain can then use to encode values of the unknown variables that better represent the sensory input [4]. While Bayesian inference and predictive coding are separate concepts, they work in tandem to create a holistic representation of human cognition. Bayesian predictive coding can be understood by first examining how these constituent models work.
BAYESIAN INFERENCE
In many situations, it is impossible to know the external cause for certain sensory stimuli. In order to eliminate some of this uncertainty, the brain must have some method of making inferences about its environment. The optimal strategy for doing so is using probabilities through Bayesian inference [4]. Although Bayesian inference is more generally used in data analysis, there is considerable evidence that human and animal behavior use Bayesian inference to achieve near-optimal performance in a variety of situations, from decision-making to learning to motor control [4]. Bayesian inference is the probability of a certain hypothesis, given a set of data [2, 3, 4, 6]. It uses both known information, called “priors,” and current incoming stimuli to form a prediction about the cause of the incoming stimuli, known as the latent (unknown) variable. The resulting prediction is known as the posterior probability, which gives the probability of each conceived latent variable being the cause of the observed sensory data. In summary, the priors are used to give baseline probabilities to the latent variables, while the incoming stimuli are used to update these probabilities to better represent the current situation [2, 3, 4, 6]. The computed posterior probability can then be used as a prior in the future [3].
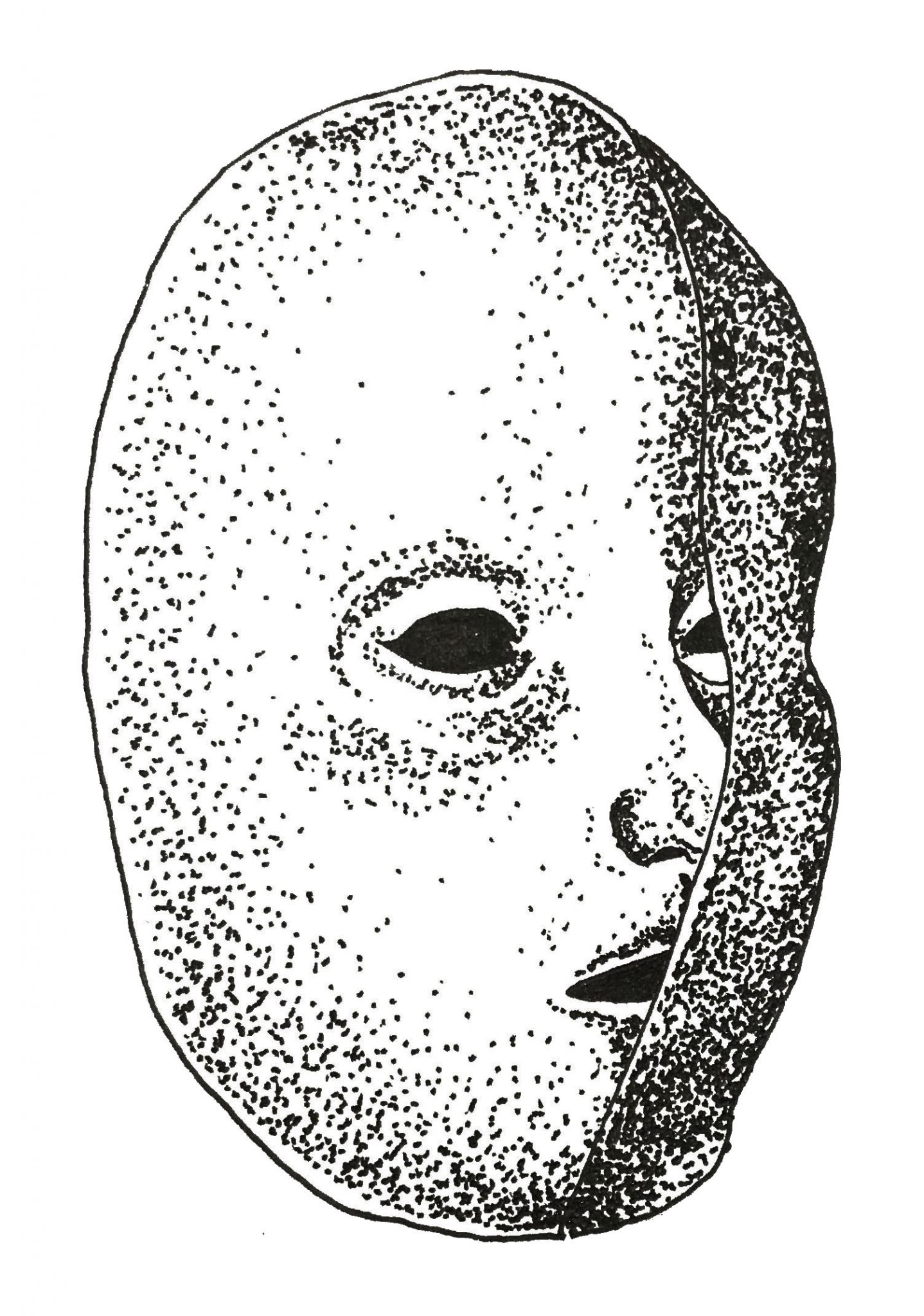
Bayesian inference also enables each prior to be weighted according to how reliable it is [2, 3]. An unreliable prior will produce a posterior probability that is based mostly on the incoming sensory data. Alternatively, a very reliable prior will resist change and produce a posterior probability that is very similar to the prior even if the stimulus contradicts it [2, 3]. This is what creates illusions [3]. For example, a mask has both a concave and a convex side; however, when watching a video of a rotating mask, both sides will appear to be convex. This is because faces are always convex, and the brain considers this fact an extremely reliable prior, so despite the incoming stimuli indicating a concave face, a convex face is perceived instead[3].
If you have heard of Sherlock Holmes, you have probably heard the saying: “When you have eliminated the impossible, whatever remains, however improbable, must be the truth” [7]. This logic is one example of Bayesian inference. When a detective arrives at a crime scene, they form an initial set of probabilities for, say, a spouse, close friends, relatives, and strangers based on similar crimes they have investigated.
This probability distribution represents the prior, and each person represents a candidate for the latent variable (the unknown cause of the crime). As the investigation continues and evidence is collected (representing the incoming sensory data), the probability of each person having committed the crime is revised, creating the posterior probability. This posterior probability will be considered the prior for the next piece of evidence. The probabilities are continuously updated throughout the investigation until no more evidence can be found, and one person has a high, relative probability of having committed the crime. The resulting suspect may have been considered improbable if they were one of the least likely candidates at the beginning of the investigation. However, once all evidence has been considered, the resulting probability distribution is the most accurate it can be for that situation. This cycle of predicting and updating beliefs is used by the brain continuously, with every movement and new sensation as evidence of the individual’s surroundings [6].
PREDICTIVE CODING
Predictive coding is a prominent model describing how the brain can perform Bayesian inference [3]. Predictive coding uses prediction errors to minimize the amount of actual sensory information transmitted to the brain to optimize the integration of sensory information [4]. A prediction error is the difference between the actual and expected incoming sensory information [3, 4]. The prediction errors can be transmitted to the brain instead of the original sensory signals to improve the efficiency of signal transmission and the acquisition of sensory data [1, 4]. Because prediction errors have a smaller range of possible values, they can be transmitted with greater accuracy using the same transmission rate [1, 4].

Predictive coding assumes a hierarchical brain structure [2, 3, 5]. Higher levels are considered to be the parts of the brain that create complex cognition, and the lower levels are the neurons that directly receive external sensory stimuli [3]. Predictive signals originating at higher levels convey expected incoming sensory data to the lower levels while lower levels send prediction errors back to the higher levels. These prediction errors can be used to determine the accuracy of the predictions. A condition known as phantom limb, in which an amputee experiences sensations in their missing limb, can be explained through predictive coding and its hierarchical structure. In this case, there are no longer nerves to make up the lower levels of the structure, so there are no prediction errors to contradict the predicted sensations that are coming from the higher levels of the brain [3].
Another prominent example of predictive coding is in the retina [1, 4]. During visual perception, the retina receives information about the spatial distribution of the intensity and wavelength of light [1]. The information accurately predicted by the brain is removed from the transmitted signal to reduce the amplitude, allowing for more efficient transmission [1]. As stated before, a prediction error is sent to the higher levels of the brain; however, predictive coding on its own does not determine how the predictions are made or how the prediction errors are used [4]. This is where Bayesian inference comes in.
BAYESIAN PREDICTIVE CODING
Bayesian inference uses the prediction errors given by predictive coding to accurately represent sensory input while predictive coding uses Bayesian predictions to calculate the prediction errors [4]. Together, these models create Bayesian predictive coding [3, 4, 5]. The lower structures in Bayesian predictive coding models use a combination of direct coding neurons, neurons that transmit the actual sensory information that is used to create accurate predictions, and predictive coding neurons, neurons that only code the prediction error to increase transmission efficiency [4]. Functional magnetic resonance imaging (fMRI) has shown that there is feedback, assumed to be prediction errors, based on predictions from higher to lower-level sensory cortices [5]. These same images show that neural responses are dampened when predictions are confirmed by sensory input and are enhanced when there is a violation of the predictions. This limits unnecessary attention to predictable stimuli [5]. An example of this is sensory adaptation or desensitization. When a person encounters a persistent stimulus such as a buzzing sound, the sound may be distracting at first. As the stimulus continues, the person will no longer perceive the sound because it can be accurately predicted by the brain. However, they will notice when the buzzing stops because the prediction of the sound is violated, increasing their attention.
Previously, both Bayesian inference and predictive coding have been used in predicting something that already occurred; however, Bayesian predictive coding can also be used as a forward model, which predicts the sensory consequences of self-produced actions [2, 3, 4, 5]. Bayesian predictive coding does this by modeling ourselves as agents who change the world around us [2, 3, 4, 5]. A simple example of the forward model is why individuals cannot tickle themselves [2, 4]. The brain is able to predict the sensory effects of the movement and therefore dulls the stimuli so an individual does not react the same way as when someone else tickles them [2, 4].
APPLICATION IN PSYCHOSIS
The forward model explained above is termed corollary discharge and plays a role in many forms of psychosis [3, 5]. Psychosis has been associated with a greater resistance to illusions, an impaired corollary discharge, improved tracking of unpredictable changes in motion, and other symptoms that directly relate to Bayesian predictive coding [5].

Most current models for psychosis focus on one specific symptom; however, it is very common to see a co-occurrence of many symptoms at varying degrees. Bayesian predictive coding may provide a framework that combines the neurobiology and the experience of psychosis through computational processes [5]. Bayesian predictive coding is unique from other models because it captures many different types of behavior, including what seems like suboptimal behavior [3]. This is because there is always a set of priors that produce what Bayesian predictive coding would denote as optimal, meaning even pathological behavior can be modeled as the result of Bayesian predictive coding [3]. As mentioned earlier, priors are weighted based on their relative reliability, and a failure to properly balance priors with sensory evidence may be a common theme in many neuropsychiatric disorders [2, 3, 5]. When either priors or sensory data are given more weight than they should, the individual no longer has an accurate view of reality [3, 5].
LIMITATIONS
While Bayesian inference and predictive coding work well in concert, that is not the only possible model for neural coding and dynamics. Bayesian inference can be performed by many other neural algorithms and representations, and predictive coding performs a useful function that can achieve a variety of computational goals [4]. It is possible to explain some of the above examples of Bayesian predictive coding with other models; however, each one requires a different method [4]. Bayesian models sometimes require complex calculations, and it is possible that humans are not capable of these calculations [2]. In that case, people may use an approximate inference, which would not be fully Bayesian, though it would utilize the same concepts. Approximate inferences could also be used to explain suboptimal behavior [2]. Because Bayesian predictive coding can include both direct coding neurons and predictive coding neurons, the model is not necessarily fully based on predictive coding [4]. It is noted earlier that predictive coding, including Bayesian predictive coding, assumes a hierarchical brain structure [2, 3, 5]. The case might be that only certain levels exhibit this model [2]. For instance, Bayesian predictive coding could explain the neural level of cognition while the system as a whole could exhibit non-Bayesian behavior or vice versa [2].
CONCLUSION
Bayesian predictive coding is one of many models used to explain neural coding and dynamics. While it does not contradict other models, its unique method of calculations allows it to explain a comparatively wide variety of behavior. Modeling human cognition has many applications not only in understanding how the brain works, but also in constructing artificial intelligence that mimics human computation and behavior. Bayesian-based probability programming could be revolutionary for machine intelligence for multiple reasons [8]. It allows for rapid prototyping and testing of different models of data, and it cuts out difficult, time-consuming parts of the programming process. Probability approaches have only recently become popular and will continue to play a central role in the development of artificial intelligence systems [8]. Assuming Bayesian predictive coding uses both direct coding neurons and predictive coding neurons, research needs to be done to reveal the location of these neural coding pathways anatomically and physiologically in existing neural cell types [4]. Further research can also be done to determine a more precise role of Bayesian predictive coding in both cognition in general and specific neurological disorders.
[1] Spratling, M.W. (2017). A review of predictive coding algorithms, Brain and Cognition, 112, 92-97, doi.org/10.1016/j.bandc.2015.11.003.
[2] Jacobs, R. A., & Kruschke, J. K. (2010). Bayesian learning theory applied to human cognition. Wiley Interdisciplinary Reviews: Cognitive Science, 2, 8–21. doi.org/10.1002/wcs.80.
[3] Parr, T., Rees, G., and Friston, K.J. (2018). Computational Neuropsychology and Bayesian Inference. Frontiers in Human Neuroscience, 12:61. doi.org/10.3389/fnhum.2018.00061.
[4] Aitchison, L., Lengyel, M. (2017). With or without you: predictive coding and Bayesian inference in the brain. Current Opinion in Neurobiology, 46, 219-227. doi.org/10.1016/j.conb.2017.08.010.
[5] Sterzer, P., et al. (2018). The Predictive Coding Account of Psychosis. Biological psychiatry, 84(9), 634-643. doi.org/10.1016/j.biopsych.2018.05.015.
[6] Kruschke, J.K. & Liddell, T.M. (2018). Bayesian data analysis for newcomers. Psychonomic Bulletin & Review, 25(1), 155-177. doi.org/10.3758/s13423-017-1272-1.
[7] Doyle, D.C. (1890). Sherlock Holmes Gives a Demonstration. The Sign of Four (pp. 68). Chicago.
[8] Ghahramani, Z. (2015). Probabilistic machine learning and artificial intelligence. Nature, 521, 452-459. doi:10.1038/nature14541.
